Dans la suite de cette page, on notera x 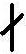 y le fait que x ne divise pas y.
y le fait que x ne divise pas y.
On notera (x_1, x_2,..., x_n) 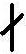 (y_1, y_2,..., y_n) la conjonction de faits suivante :
(y_1, y_2,..., y_n) la conjonction de faits suivante :
x_1 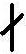 y_1 y_1 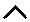 |
x_2 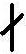 y_2 y_2 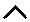 |
...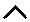 |
x_n 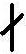 y_n y_n |
Par exemple, (2, 3, 4) 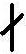 (3,2,1) et c'est d'ailleurs pour cette raison que 3 est décomposant Goldbach de 8.
(3,2,1) et c'est d'ailleurs pour cette raison que 3 est décomposant Goldbach de 8.
De même, 3 est décomposant Goldbach de 10 car (2,3,4,5) 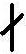 (5,4,3,2).
(5,4,3,2).
Ou bien, 5 est décomposant Goldbach de 12 car (2,3,4,5,6) 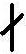 (5,4,3,2,1).
(5,4,3,2,1).
Ou encore, 3 est décomposant Goldbach de 20 car (2,3,4,..,10) 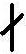 (15,14,13,..,7).
(15,14,13,..,7).
Ou encore, 7 est décomposant Goldbach de 20 car (2,3,4,..,10) 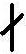 (11,10,9,..,3).
(11,10,9,..,3).
Pour 2x = 40, on a mis dans le tableau suivant dans la première ligne la suite des nombres entiers croissants de 2 à x=20 et dans les lignes suivantes les suites d'entiers décroissants correspondant aux nombres premiers 3, 5, 7, 11, 13, 17 et 19. On a colorié dans les lignes un nombre divisible par sa tête de colonne, ce qui empêche le nombre premier de sa ligne de fournir une décomposition Goldbach de 2x.
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| ligne du nombre premier 3 |
35 |
34 |
33 |
32 |
31 |
30 |
29 |
28 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
| ligne du nombre premier 5 |
33 |
32 |
31 |
30 |
29 |
28 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
16 |
15 |
| ligne du nombre premier 7 |
31 |
30 |
29 |
28 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
16 |
15 |
14 |
13 |
| ligne du nombre premier 11 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
| ligne du nombre premier 13 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
| ligne du nombre premier 17 |
21 |
20 |
19 |
18 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
| ligne du nombre premier 19 |
19 |
18 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
Cela ne devrait pas poser beaucoup de problèmes à Terence Tao de prouver que quelque soit 2x un nombre pair, il existe toujours une suite décroissante de x-1 nombres entiers successifs et inférieurs strictement à 2x-1 qui n'est pas divisible par la suite (2, 3,...,x). Il y a peut-être également moyen de s'inspirer du paragraphe 9 du tome 2 de la théorie des nombres de Legendre dont voici les pages :![]() y le fait que x ne divise pas y.
y le fait que x ne divise pas y. ![]() (y_1, y_2,..., y_n) la conjonction de faits suivante :
(y_1, y_2,..., y_n) la conjonction de faits suivante :
![]() y_1
y_1 ![]()
![]() y_2
y_2 ![]()
![]()
![]() y_n
y_n![]() (3,2,1) et c'est d'ailleurs pour cette raison que 3 est décomposant Goldbach de 8.
(3,2,1) et c'est d'ailleurs pour cette raison que 3 est décomposant Goldbach de 8.![]() (5,4,3,2).
(5,4,3,2).![]() (5,4,3,2,1).
(5,4,3,2,1). ![]() (15,14,13,..,7).
(15,14,13,..,7).![]() (11,10,9,..,3).
(11,10,9,..,3).