|
On sait que l'ensemble des unités de n (ensembles des nombres inférieurs à n et premiers à lui) muni de la multiplication est un groupe.
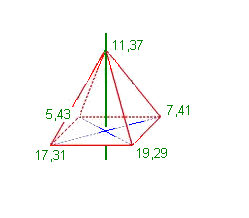
Cet été, j'ai fait des calculs et des découvertes qui m'ont amenée tout droit dans la théorie des groupes. Je trouve ces découvertes très esthétiques, même si elles ne constituent pour l'instant que des exemples à approfondir. Les voici. Je cherchais par tous les moyens à relier entre elles les décompositions Goldbach. J'avais pris pour habitude d'identifier un nombre premier et son complémentaire à 2x (ça consiste à passer à l'ensemble-quotient pour la relation d'équivalence définie par x R y ssi x+y=2x), et j'ai trouvé pour certains nombres pairs des polyèdres de dimension le nombre de décompositions Goldbach de la façon suivante : Considérons le nombre 36 et ses 4 décompositions 13+23, 5+31, 7+29, 17+19. Imaginons que ces 4 décompositions se trouvent être les 4 sommets d'un tétraèdre qui aurait un axe passant par le sommet (13,23) et une base passant par les trois autres sommets. Multiplier les sommets de la base de la pyramide par le sommet qui est sur l'axe fait tourner la base d'un angle de 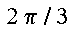 . .Selon le même principe, on trouve un tétraèdre pour le nombre pair 42 à 4 décompositions également.
Cette idée de représentation géométrique des groupes de permutations se retrouve dans l'article d'Alain Connes "Symétries" du Pour la Science n° 292 de février 2001 (http://www.alainconnes.org/docs/symetries.pdf, en anglais Symmetries, Newsletter de l'European Mathematical Society, n°54, p. 11, décembre 2004 https://www.ems-ph.org/journals/newsletter/pdf/2004-12-54.pdf), ou dans le livre de Jean Sivardière (Description de la symétrie, EDP Sciences, 2004), ou dans le numéro spécial Les génies de la science, aux éditions Pour la Science, consacré à Galois (Norbert Verdier, mai 2011) . On trouve d'autre part une pyramide à base carrée pour le nombre 48 à 5 décompositions. La base "tourne" autour de l'axe (par multiplication par le sommet) d'un angle  . .
On trouve un octaèdre pour le nombre 60 à 6 décompositions. Le sommet "du haut" fait tourner les 4 sommets "médians" d'un angle de  dans un sens, tandis que le sommet "du bas" fait tourner les 4 sommets en question dans l'autre sens. dans un sens, tandis que le sommet "du bas" fait tourner les 4 sommets en question dans l'autre sens.
On trouve une pyramide à base pentagonale pour 66 à 6 décompositions également. La base tourne bien sûr d'un angle  . .
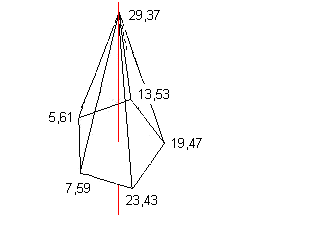
Enfin, j'ai inventé le noeud papillon rotatif pour 78 et le tipi hexagonal pour 96 qui ont les formes suivantes :
Pour le tipi hexagonal, le sommet (17,79) "envoie" (37,59) sur (43,53) et inversement et fait de même avec les deux autres couples de sommets. Il se trouve que les polyèdres concernent à chaque fois : - des nombres multiples de 6, - des nombres qui sont les plus petits à avoir un certain nombre de décompositions Goldbach. Enfin, j'ai étudié le cas de 84 qui a résisté longtemps et qui a fini par me fournir ses polyèdres associés : ce sont des polyèdres sur des nombres premiers mais tous ces nombres premiers ne participent pas forcément à des décompositions Goldbach de 84.
Toutes ces structures proviennent de propriétés des racines n-ièmes de l'unité dans le groupe des unités du nombre pair considéré. Ces propriétés entraînent parfois l'obtention d'un polyèdre dont les sommets sont tous décomposants Goldbach, parfois, ce n'est pas le cas. En tous cas, c'est très joli... En cliquant sur le lien ci-dessous seront fournies quelques pistes concernant les groupes des unités.

 |


 13 (mod 42)
13 (mod 42)