|
L'idée de réfléchir du côté des polynômes est venue de la lecture d'un article du livre de Ian Gordon intitulé "le théorème de Noël" et qui présente le domaine de la "géométrie des nombres" dont Minkowski est à l'origine. On peut imaginer que les solutions Goldbach (les nombres premiers fournissant une décomposition Goldbach d'un nombre pair donné) sont les solutions d'équations polynomiales particulières (dans l'anneau du nombre pair considéré, peut-être).
Par exemple, dans Z17, 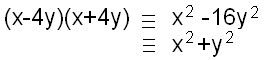 . .Autre exemple, dans Z4, le monôme x+2 divise 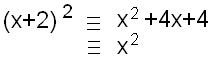 . .Au niveau bibliographique, on trouve sur Gallica un mémoire d'Abel intitulé "mémoire sur une classe particulière d'équations résolubles par radicaux". On trouve également un article de Galois "Sur la théorie des nombres", dans le Journal de mathématiques, p.398 (Bulletin de Ferussac, tome XIII p.428, année 1830, cahier de juin). Deux extraits de ce texte seraient à bien comprendre : "Le principal avantage de la nouvelle théorie que nous venons d'exposer est de ramener les congruences à la propriété (si utile dans les équations ordinaires) d'admettre précisément autant de racines qu'il y a d'unités dans l'ordre de leur degré". ... "Ensuite, pour avoir les solutions entières, il suffira, ainsi que M.Libri paraît en avoir le premier fait la remarque, de chercher le plus grand facteur commun à Fx=0 et à x^(p-1)=1.". Enfin, pour clore ces idées bibliographiques, il faudrait aussi bien comprendre le "traité des substitutions et des équations algébriques" de Camille Jordan. En lisant, et fouillant la toile, je me suis focalisée sur deux sortes de polynômes : les polynômes symétriques (au début, j'avais lu un chapitre dans la théorie des nombres de Lucas, qui s'intitulait "les fonctions symétriques") et les polynômes cyclotomiques dans un deuxième temps (on trouve dans l'article de Wikipédia concernant ces derniers que leur groupe de Galois est commutatif et cyclique et pour certains nombres pairs, c'est exactement les propriétés de leur groupe des unités muni de la multiplication). Dans l'article "racine de l'unité" de Wikipédia, on peut lire "En adjoignant une racine primitive n-ième de l'unité à Q, nous obtenons le corps n-cyclotomique Fn. Ce corps contient toutes les racines n-ièmes de l'unité et est le corps de décomposition sur Q du polynôme cyclotomique d'indice n. L'extension de corps Fn/Q est de degré  et son groupe de Galois est naturellement isomorphe au groupe multiplicatif des inversibles de l'anneau Z/nZ". et son groupe de Galois est naturellement isomorphe au groupe multiplicatif des inversibles de l'anneau Z/nZ".Quand je me suis découragée de trouver quoi que ce soit, tant la littérature est hermétique, j'ai mis mon dernier courage dans de multiples calculs, dont j'espérais qu'ils m'éclaireraient un peu. Pour ce qui est des polynômes symétriques, on trouve qu'ils peuvent tous s'exprimer en fonction de certains polynômes qu'on appelle les polynômes élémentaires et pour ceux-là, c'est assez simple : il faut calculer la somme des racines (qu'on notera S1), ou la somme des produit deux à deux des racines (qu'on notera S2), ou la somme des produits trois à trois des racines (qu'on notera S3), etc, et ça, je peux le faire avec les "solutions Goldbach". Pour 36, les solutions sont 5, 7, 13 et 17. S1=42. S2=616. S3=3702. S4=7735. La somme de ces nombres est congrue à -1 modulo 36. Est-ce normal ? Si on calcule -S1+S2-S3+S4, on retrouve une congruence à -1. Pour 40, les solutions sont 3, 11 et 17. S1=31. S2=271. S3=561. S1-S2+S3 est congru à l'unité modulo 40. Pour 42, les racines dont le produit vaut 1 sont 5, 11, 13 et 23. S1=52. S2=930. S3=6764. S4=16445. S1+S2+S3+S4 est congru à -1. Pour 48, les racines dont le produit vaut 1 sont 5, 7 et 11. S1=23. S2=167. S3=385. S4=16445. S1+S2+S3 est congru à -1. Pour 50, les racines dont le produit vaut 1 sont 3, 7, 13 et 19. S1=42. S2=588. S3=3142. S4=5187. Pas de congruence à l'unité. Par contre, si au lieu de S1=42, on prend S1=16 (provenant de 3+7-13+19), S1+S2-S3+S4, on retrouve la congruence à -1. Pour 52, les racines dont le produit vaut 1 sont 5, 11, et 23. S1=39. S2=423. S3=1265. Pas de congruence. Par contre, si au lieu de S1=39, on prend S1=29 (provenant de -5+11+23) S1+S2+S3 est congru à 1. Pour 64, les racines dont le produit vaut 1 sont 5, 11, 17 et 23. S1=56. S2=1086. S3=8456. S4=21505. S1+S2+S3+S4 est congru à -1. Pour 66, les racines dont le produit vaut 1 sont 5, 13, 19, 23 et 29. S1=89. S2=2998. S3=47078. S4=335689. S5=823745. S1-S2+S3-S4+S5 est congru à +1. Pour 72, les racines dont le produit vaut -1 sont 5, 11, 19, 29 et 31. S1=95. S2=3358. S3=54050. S4=385441. S5=939455. S1-S2+S3-S4+S5 est congru à +1. |